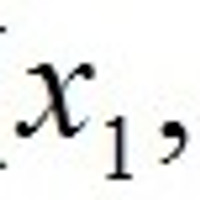한동안 공부에 손을 놓았더니....ㅠ.ㅠ 기본적인 수학도 기억이 않난다.
일단 기본적인 것 부터 다시 보고 넘어간다.
다음과 같은 함수는 2차원으로 그래프로 표시하기 쉽다.
 만약 정의역이 2개의 변수로 구성이 되면 조금 복잡해 지는데, z = f(x,y)의 형태로 표기하게 된다. 예를 들어 아래와 같은 함수를 그래프로 표현하여 보면,
만약 정의역이 2개의 변수로 구성이 되면 조금 복잡해 지는데, z = f(x,y)의 형태로 표기하게 된다. 예를 들어 아래와 같은 함수를 그래프로 표현하여 보면,

clf
x = -2:0.2:2;
y = -2:0.2:2;
[x,y] = meshgrid(x,y);
z = x.^2-y.^2;
mesh(x,y,z)

이런 모양이 되겠다.
보통 한개의 변수로 이루어진 함수를 미분할려면 아래 식과 같이 그냥 하면된다.

하지만 변수가 2개 이상이 되면, partial derivative(편도함수) 로 표현한다.
x의 편도함수

y의 편도함수
이다. 이걸 좀 더 간편하게 표현하면 아래와 같이 표현할 수 있겠다.

두번 미분때리냐 3번 미분 때리냐에 따라서 2계편도함수, 3계편도함수라고 말을 하고, 변수에 따라서 미분계수가 다를경우 복합편도함수라고 한다.
2계편도함수의 기하학적 의미를 살펴보면,
아래의 그림에서 y=f(u,v)라는 함수가 있다. 이는 2개의 변수를 가지고 있는 함수이기 때문에, 그림과 같이 2차원 평면의 면으로 그려진다. 좌측의 그림에서 C1은 y=f(u,v)함수를 v0에서 자른 단면의 모습이다. 우즉 그림의 C2도 마찬가지로 u0에서 달린 단면의 모습이다. 즉, y함수의 u0,v0에서의 기울기는 u축 기준의 기울기와 v축 기준의 기울기를 모두 가지고 있고, u0,v0에서의 각각의 기울기는 fu(u0,v0)와 fv(u0,v0)가 된다.

[참조]
http://pinkwink.kr/206
http://psahnwoo.blog.me/110105012447
일단 기본적인 것 부터 다시 보고 넘어간다.
다음과 같은 함수는 2차원으로 그래프로 표시하기 쉽다.
x = -2:0.2:2;
y = -2:0.2:2;
[x,y] = meshgrid(x,y);
z = x.^2-y.^2;
mesh(x,y,z)

이런 모양이 되겠다.
보통 한개의 변수로 이루어진 함수를 미분할려면 아래 식과 같이 그냥 하면된다.

하지만 변수가 2개 이상이 되면, partial derivative(편도함수) 로 표현한다.
x의 편도함수

y의 편도함수

이다. 이걸 좀 더 간편하게 표현하면 아래와 같이 표현할 수 있겠다.

두번 미분때리냐 3번 미분 때리냐에 따라서 2계편도함수, 3계편도함수라고 말을 하고, 변수에 따라서 미분계수가 다를경우 복합편도함수라고 한다.
아래의 그림에서 y=f(u,v)라는 함수가 있다. 이는 2개의 변수를 가지고 있는 함수이기 때문에, 그림과 같이 2차원 평면의 면으로 그려진다. 좌측의 그림에서 C1은 y=f(u,v)함수를 v0에서 자른 단면의 모습이다. 우즉 그림의 C2도 마찬가지로 u0에서 달린 단면의 모습이다. 즉, y함수의 u0,v0에서의 기울기는 u축 기준의 기울기와 v축 기준의 기울기를 모두 가지고 있고, u0,v0에서의 각각의 기울기는 fu(u0,v0)와 fv(u0,v0)가 된다.

[참조]
http://pinkwink.kr/206
http://psahnwoo.blog.me/110105012447